Autonomous Robotic Manipulation as a Partially Observable Markov Decision Process- Juniper Publishers
Juniper Publishers- Journal of Robotics
Abstract
Object manipulation is the most significant and
challenging way for a robot to interact with its environment. It often
requires computation on different channels of sensory information and
the use of sophisticated controllers that can quickly lead to
intractable solutions. In recent years, increasingly uncertain work
spaces have lead researchers to turn to Partially Observable Markov
Processes for robotic manipulation. The frame works provide methods to
find an optimal sequence of actions to follow based on state belief and a
partially observed world. This paper reviews the use of POMDP in the
literature and points to fundamental papers on the subject.
Keywords: POMDP; Robotic manipulation
Abbreviations: POMDP: Partially Observable Markov Decision Process; RL: Reinforcement Learning
Introduction
Robots are increasingly expected to be more than
mindless tools that are programmed to do one task in one particular way.
They must perform in domestic/human environments and respond
intelligently to high level command such as "make me dinner” or "find my
phone”. Nonetheless, the uncertainty of these environments, unreliable
sensory data and the difficulty in transforming a high level task to a
low level manipulation problem makes this premise a challenging one.
Manipulation and task planning capabilities for robotic systems are by
consequence a vibrant subject of research at the present time.
POMDP [1]
is a promising framework that integrates robotic manipulation and task
planning and allows robots to develop sophisticated behaviour based on
the user defined goals. It is formulated as the tuple <S; A; T; R; O;
Z> where S, the state space of the process, is the collection of all
system states. Depending of the application, the state space may be
multi dimensional containing both information on the robot
(configuration, joint torque, etc...) and on the workspace acquired
through sensors (Tactile, Force/Torque, Depth Camera, etc...). A is the
action space, consisting of all the actions available to the robot such
as input torques on a joint or the movement of a certain object (macro
actions [2]).
An action a ∈ A leads to a state transition which is non-deterministic
and described by T. In scenarios where the transition cannot be
described analytically, they can be learned through experience [3].
R, the reward function, assigns a positive or negative numerical value
to actions taken in specific parts of the state space. Rewards allow the
robot to converge towards the desired goal and to stay away from
undesirable situations, the process known as reward shaping. 0 ∈ O is
the observation space, that generally consist of information received
from the sensors on the robots. The reliability of an observation o 2 O
is embedded in Z, the observation function, which gives the probability
of an observation being accurate. It corresponds to the partially
observable aspect of the process.
Since the states of the system are only partially
observable, POMDPs reason on a belief, b(s) = Pr (s\o,a) rather than the
states themselves. The belief is a probability density function over
the state space making it continuous. The axioms of probability dictate
that 0 ≤ b (s)≤ 1 and that Σs∈sb (s ) = 1 [1]. Upon taking an action and receiving an observation, a new belief b' can be recovered using a Bayes filter:
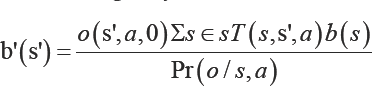 This part of the process is often referred to as the state estimator SE.
The second part of a partially observable Markov
decision process is to find the optimal action to take based on the
current belief. The Bellman equation [1]
can be used to compute the value of a belief state which is based on
the immediate reward received for taking an action in a certain state
and the expected future reward over a defined horizon. Keeping track of
the belief and searching for an optimal action through the state,
observation and action space becomes rapidly expensive. Recent
algorithms such as point-based value iteration [4] and SARSOP [5] only consider parts of the belief to make the computations tractable.
Section II of this paper elaborates on a few
applications of POMDPs specifically for manipulation tasks and section
III concludes the paper.
This part of the process is often referred to as the state estimator SE.
The second part of a partially observable Markov
decision process is to find the optimal action to take based on the
current belief. The Bellman equation [1]
can be used to compute the value of a belief state which is based on
the immediate reward received for taking an action in a certain state
and the expected future reward over a defined horizon. Keeping track of
the belief and searching for an optimal action through the state,
observation and action space becomes rapidly expensive. Recent
algorithms such as point-based value iteration [4] and SARSOP [5] only consider parts of the belief to make the computations tractable.
Section II of this paper elaborates on a few
applications of POMDPs specifically for manipulation tasks and section
III concludes the paper.
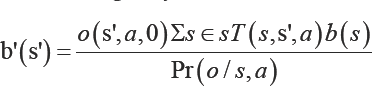


Comments
Post a Comment