Differential Evolution (DE): A Short Review- Juniper Publishers
Juniper Publishers-Journal of Robotics
Abstract
Proposing new mutation strategies and adjusting
control parameters to improve the optimization performance of
differential evolution (DE) are considered a vital research study.
Therefore, in this paper, a short review of the most significant
contributions on parameter adaptation and developed mutation strategies
is presented.
Keywords: Evolutionary computation; Global optimization; Differential evolution; Mutation strategy; Adaptive parameter control
Abbreviations: DE:
Differential Evolution; EAs: Evolutionary Algorithms; CR: Crossover
Rate; SF: Scaling Factor; FADE: Fuzzy Adaptive Differential Evolution;
SDE: Self Adaptive Differential Evolution
Introduction
Differential Evolution (DE), proposed by Storn and Price [1,2]
is a stochastic population-based search method. It exhibits excellent
capability in solving a wide range of optimization problems with
different characteristics from several fields and many real-world
application problems [3].
Similar to all other Evolutionary algorithms (EAs), the evolutionary
process of DE uses mutations, crossover and selection operators at each
generation to reach the global optimum. Besides, it is one of the most
efficient evolutionary algorithms (EAs) currently in use. In DE, each
individual in the population is called target vector. Mutation is used
to generate a mutant vector, which perturbs a target vector using the
difference vector of other individuals in the population. After that,
crossover operation generates the trial vector by combining the
parameters of the mutation vector with the parameters of a parent vector
selected from the population. Finally, according to the fitness value
and selection operation determines which of the vectors should be chosen
for the next generation by implementing a one-to-one completion between
the generated trail vectors and the corresponding parent vectors [4,5].
The performance of DE basically depends on the mutation strategy, the
crossover operator. Besides, The intrinsic control parameters
(population size NP, scaling factor F, the crossover rate CR) play a
vital role in balancing the diversity of population and convergence
speed of the algorithm. The advantages are simplicity of implementation,
reliable, speed and robustness [3].
Thus, it has been widely applied in solving many real-world
applications of science and engineering, such as {0-1} Knapsack Problem [6], financial markets dynamic modeling [7], feature selection [8], admission capacity planning higher education [9,10] , and solar energy [11], for more applications, interested readers can refer to [12].
However, DE has many weaknesses, as all other evolutionary search
techniques do w.r.t the NFL theorem. Generally, DE has a good global
exploration ability that can reach the region of global optimum, but it
is slow at exploitation of the solution [13].
Additionally, the parameters of DE are problem dependent and it is
difficult to adjust them for different problems. Moreover, DE
performance decreases as search space dimensionality increases [14].
Finally, the performance of DE deteriorates significantly when the
problems of premature convergence and/or stagnation occur [14,15]. Consequently, researchers have suggested many techniques to improve the basic DE. From the literature [12,16,17],
these proposed modifications, improvements and developments on DE focus
on adjusting control parameters in an adaptive or self-adaptive manner
while there are a few attempts in developing new mutations rule.
Differential Evolution
This section provides a brief summary of the basic
Differential Evolution (DE) algorithm. In simple DE, generally known as
DE/rand/1/bin [2,18], an initial random population, denoted by P, consists of NP individual. Each individual is represented by the vector, = (x1,i,x2,ixD,i)
where D is the number of dimensions in solution space. Since the
population will be varied with the running of evolutionary process, the
generation times in DE are expressed by G = 0,I,...,Gmax , where is the maximal time of generations. For the ith individual of P at the G generation, it is denoted by xGi = (xG1,i, xG2,i,..., xGD,i) . The lower and upper bounds in each dimension of search space are respectively recorded by xL = (x1,L, x2,L,..., xD,L) and xu = (xl, u, x2,u,..., xD,u ). The initial population P0is randomly generated according to a uniform distribution within the lower and upper boundaries (xL ,xu).
After initialization, these individuals are evolved by DE operators
(mutation and crossover) to generate a trial vector. A comparison
between the parent and its trial vector is then done to select the
vector which should survive to the next generation [16,19]. DE steps are discussed below:
Initialization
In order to establish a starting point for the optimization process, an initial population P0 must be created. Typically, each jth component (j = l,2,..... ,D) of the ith individuals (i = 1,2, ...., NP) in the P0 is obtained as follow:
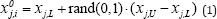
Where, rand (0,1) returns a uniformly distributed random number in [0,1].
Mutation
At generation G, for each target vector, a mutant vector is generated according to the following:

With randomly chosen indices r1r2,r3∈{1,2,...,NP}. is a real number to control the amplification of the difference vector (xGr2 -xGr3) . According to Storn and Price [2],
the range of is in (0,2). In this work, If a component of a mutant
vector violates search space, then the value of this component is
generated a new using (1). The other most frequently used mutations
strategies are
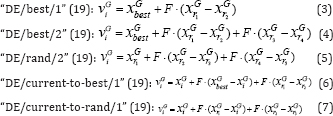
The indices r1, r2, r3, r4, r5
are mutually different integers randomly generated within the range
(1,2,...,NP), which are also different from the index . These indices
are randomly generated once for each mutant vector. The scale factor is a
positive control parameter for scaling the difference vector. xGbest is the best individual vector with the best fitness value in the population at generation G.
Cross Over
There are two main crossover types, binomial and
exponential. We here elaborate the binomial crossover. In the binomial
crossover, the target vector is mixed with the mutated vector, using the
following scheme, to yield the trial vector.
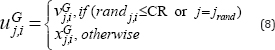
Where, (i ∈[1, NP] and j ∈ [1,D]) is a uniformly distributed random number in (0,1) CR ∈ [0,1] , called the crossover rate that controls how many components are inherited from the mutant vector jrand
, is a uniformly distributed random integer in (1,D) that makes sure at
least one component of trial vector is inherited from the mutant
vector.
Selection
DE adapts a greedy selection strategy. If and only if the trial vector uGi yields as good as or a better fitness function value than xGi , then uGi is set to xG+1i . Otherwise, the old vector xGi is retained. The selection scheme is as follows (for a minimization problem):
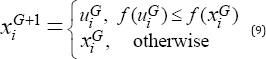
A detailed description of standard DE algorithm is given in Figure 1.

Rand int (min, max) is a function that returns an integer number between min and max.
NP, Gmax, CR and F are user-defined parameters. D is the dimensionality of the problem.
Short Review
Virtually, the performance of the canonical DE
algorithm mainly depends on the chosen mutation/crossover strategies and
the associated control parameters. Moreover, due to DE limitations as
previously aforementioned in introduction section, during the past 15
years, many researchers have been working on the improvement of DE.
Thus, many researchers have proposed novel techniques to overcome its
problems and improve its performance [16].
In general, According to adjusting control parameters rule used, these
approaches can be divided into two main groups: The first group focuses
on pure random selection of parameter values from random distributions
such as the uniform distribution, normal distribution, and Cauchy
distribution. Alternatively, the parameters values are changing with the
progress of generations using increasing/decreasing linear or nonlinear
deterministic function such as. The second group focuses on adjusting
control parameters in an adaptive or self-adaptive manner. A brief
overview of these algorithms is proposed in this section. Firstly, many
trial-and-errors experiments have been conducted to adjust the control
parameters. Storn and Price [1]
suggested that NP (population size) between 5D and 10D and 0.5 as a
good initial value of F (mutation scaling factor). The effective value
of F usually lies in a range between 0.4 and 1. The CR (crossover rate)
is an initial good choice of CR=0.1; however, since a large CR often
accelerates convergence, it is appropriate to first try CR as 0.9 or 1
in order to check if a quick solution is possible. Gamperle at al. [20] recommended that a good choice for NP is between 3D and 8D, with F=0.6 and CR lies in (0.3, 0.9). However, Rokkonen et al. [21]
concluded that F=0.9 is a good compromise between convergence speed and
convergence rate. Additionally, CR depends on the nature of the
problem, so CR with a value between 0.9 and 1 is suitable for
non-separable and multimodal objective functions, while a value of CR
between 0 and 0.2 when the objective function is separable. On the other
hand, due to the apparent contradictions regarding the rules for
determining the appropriate values of the control parameters from the
literature, some techniques have been designed with a view of adjusting
control parameters in adaptive or self-adaptive manner instead of manual
tuning procedure. Zaharie [22]
introduced an adaptive DE (ADE) algorithm based on the idea of
controlling the population diversity and implemented a multi-population
approach. Liu et al. [23]
proposed a Fuzzy Adaptive Differential Evolution (FADE) algorithm.
Fuzzy logic controllers were used to adjust F and CR. Numerical
experiments and comparisons on a set of well known benchmark functions
showed that the FADE Algorithm outperformed basic DE algorithm.
Likewise, Brest et al. [24]
proposed an efficient technique, named jDE, for self- adapting control
parameter settings. This technique encodes the parameters into each
individual and adapts them by means of evolution. The results showed
that jDE is better than, or at least comparable to, the standard DE
algorithm, (FADE) algorithm and other state of-the-art algorithms when
considering the quality of the solutions obtained. In the same context,
Omran et al. [25]
proposed a Self-adaptive Differential Evolution (SDE) algorithm. F was
self-adapted using a mutation rule similar to the mutation operator in
the basic DE. The experiments conducted showed that SDE generally
outperformed DE algorithms and other evolutionary algorithms. Qin et al.
[26]
introduced a self-adaptive differential evolution (SaDE). The main idea
of SaDE is to simultaneously implement two mutation schemes:
"DE/rand/1/bin” and "DE/ best/2/bin'' as well as adapt mutation and
crossover parameters. The Performance of SaDE evaluated on a suite of 26
several benchmark problems and it was compared with the conventional DE
and three adaptive DE variants. The experimental results demonstrated
that SaDE yielded better quality solutions and had a higher success
rate. In the same context, inspired by SaDE algorithm and motivated by
the success of diverse self-adaptive DE approaches, Mallipeddi et al. [19]
developed a self-adaptive DE, called EPSDE, based on ensemble approach.
In EPSDE, a pool of distinct mutation strategies along with a pool of
values for each control parameter coexists throughout the evolution
process and competes to produce offspring. The performance of EPSDE was
evaluated on a set of bound constrained problems and was compared with
conventional DE and other state-of-the-art parameter adaptive DE
variants. The resulting comparisons showed that EPSDE algorithm
outperformed conventional DE and other state of-the-art parameter
adaptive DE variants in terms of solution quality and robustness.
Similarly, motivated by the important results obtained by other
researchers during past years, Wang et al. [27]
proposed a novel method, called composite DE (CoDE). This method used
three trial vector generation strategies and three control parameter
settings. It randomly combines them to generate trial vectors. The
performance of CoDE has been evaluated on 25 benchmark test functions
developed for IEEE CEC2005 and it was very competitive to other compared
algorithms. Recently, Super-fit Multicriteria Adaptive DE (SMADE) is
proposed by Caraffini et al. [28],
which is a Memetic approach based on the hybridization of the
Covariance Matrix Adaptive Evolutionary Strategy (CMAES) with modified
DE, namely Multi criteria Adaptive DE (MADE). MADE makes use of four
mutation/crossover strategies in adaptive manner which are rand/1/bin,
rand/2/ bin, rand-to-best/2/bin and current-to-rand/1. The control
parameters CR and F are adaptively adjusted during the evolution. At the
beginning of the optimization process, CMAES is used to generate a
solution with a high quality which is then injected into the population
of MADE. The performance of SMADE has been evaluated on 28 benchmark
test functions developed for IEEE CEC2013 and the experimental results
are very promising. On the other hand, improving the trial vector
generation strategy has attracted many researches. In fact, DE/rand/1 is
the fundamental mutation strategy developed by Storn and Price [2,3], and is reported to be the most successful and widely used scheme in the literature [16].
Obviously, in this strategy, the three vectors are chosen from the
population at random for mutation and the base vector is then selected
at random among the three. The other two vectors form the difference
vector that is added to the base vector. Consequently, it is able to
maintain population diversity and global search capability with no bias
to any specific search direction, but it slows down the convergence
speed of DE algorithms [26].
DE/ rand/2 strategy, like the former scheme with extra two vectors that
forms another difference vector, which might lead to better
perturbation than one-difference-vector-based strategies [26].
Furthermore, it can provide more various differential trial vectors
than the DE/rand/1/bin strategy which increase its exploration ability
of the search space. On the other hand, greedy strategies like
DE/best/1, DE/best/2 and DE/current-to-best/1 incorporate the
information of the best solution found so far in the evolutionary
process to increase the local search tendency that lead to fast
convergence speed of the algorithm. However, the diversity of the
population and exploration capability of the algorithm may deteriorate
or may be completely lost through a very small number of generations
i.e. at the beginning of the optimization process, that cause problems
such stagnation and/or premature convergence. Thus, In order to improve
the convergence velocity of DE, Fan & Lampinen [18]
proposed a trigonometric mutation scheme, which is considered local
search operator, and combined it with DE/rand/1 mutation operator to
design TDE algorithm. Zhang & Sanderson [29]
introduced a new differential evolution (DE) algorithm, named JADE, to
improve optimization performance by implementing a new mutation strategy
"DE/current-to-p best” with optional external archive and by updating
control parameters in an adaptive manner. Simulation results show that
JADE was better than, or at least competitive to, other classic or
adaptive DE algorithms such as Particle swarm and other evolutionary
algorithms from the literature in terms of convergence performance.
Tanabe & Fukunaga [30] proposed an improved variant of the JADE algorithm [29]
and called the same as the Success History based DE (SHADE). In SHADE,
instead of sampling the F and Cr values from gradually adapted
probability distributions, the authors used historical memory archives
MCr and MF which store a set of Cr and F values, respectively that have
performed well in the recent past .The algorithm generates new Cr, F
pairs by directly sampling the parameter space close to one of the
stored pairs. Out of the 21 algorithms that participated in the IEEE CEC
2013 competition on real parameter single-objective optimization, SHADE
ranked 3rd, the first two ranks being taken by non-DE based algorithms.
Tanabe & Fukunaga [31]
further improved the SHADE algorithm by using the linear population
size reduction and called this variant as L-SHADE. In L-SHADE, the
population size of DE is continually reduced by means of a linear
function [16]. Mohamed et al. [32]
enhances the LSHADE algorithm by employing an alternative adaptation
approach for the selection of control parameters is proposed. The
proposed algorithm, named LSHADE-SPA, uses a new semi-parameter
adaptation approach to effectively adapt the values of the scaling
factor of the Differential evolution algorithm. The proposed approach
consists of two different settings for two control parameters F and Cr.
The benefit of this approach is to prove that the semi-adaptive
algorithm is better than pure random algorithm or fully adaptive or
self- adaptive algorithm. To enhance the performance of LSHADE- SPA
algorithm, they also introduced a hybridization framework named
LSHADE-SPACMA between LSHADE-SPA and a modified version of CMA-ES. The
modified version of CMA-ES undergoes the crossover operation to improve
the exploration capability of the proposed framework. In LSHADE-SPACMA
both algorithms will work simultaneously on the same population, but
more populations will be assigned gradually to the better performance
algorithm. Out of the 12 algorithms that participated in the IEEE CEC
2017 competition on real parameter single-objective optimization,
LSHADE-SPACMA ranked 3rd. Along the same lines, to overcome the
premature convergence and stagnation problems observed in the classical
DE, Islam et al. [33]
proposed modified DE with p-best crossover, named MDE_PBX . The novel
mutation strategy is similar to DE/current-to-best/1 scheme. It selects
the best vector from a dynamic group of q% of the randomly selected
population members. Moreover, their crossover strategy uses a vector
that is randomly selected from the p top ranking vectors according to
their objective values in the current population (instead of the target
vector) to enhance the inclusion of generic information from the elite
individuals in the current generation. The parameter p is linearly
reduced with generations to favors the exploration at the beginning of
the search and exploitation during the later stages by gradually
downsizing the elitist portion of the population. Das et al. [34]
proposed two kinds of topological neighborhood models for DE in order
to achieve better balance between its explorative and exploitative
tendencies. In this method, called DEGL, two trial vectors are created
by the global and local neighborhood-based mutation. These two trial
vectors are combined to form the actual trial vector by using a weight
factor. The performance of DEGL has been evaluated on 24 benchmark test
functions and two real-world problems and showed very competitive
results. In order to solve unconstrained and constrained optimization
problems, Mohamed et al. [35,36]
proposed a novel directed mutation based on the weighted difference
vector between the best and the worst individuals at a particular
generation, is introduced. The new directed mutation rule is combined
with the modified basic mutation strategy DE/rand/1/bin, where only one
of the two mutation rules is applied with the probability of 0.5. The
proposed mutation rule is shown to enhance the local search ability of
the basic Differential Evolution (DE) and to get a better trade-off
between convergence rate and robustness. Numerical experiments on
well-known unconstrained and constrained benchmark test functions and
five engineering design problems have shown that the new approach is
efficient, effective and robust. Similarly, to enhance global and local
search capabilities and simultaneously increases the convergence speed
of DE, Mohamed [37]
introduced a new triangular mutation rule based on the convex
combination vector of the triplet defined by the three randomly chosen
vectors and the difference vector between the best and the worst
individuals among the three randomly selected vectors.
The proposed mutation vector is generated in the following manner:
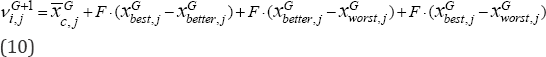
Where, XGbest , XGbetter and XGworst are the tournament best, better and worst three randomly selected vectors, respectively. The convex combination vector 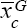 of the triangle is a linear combination of the three randomly selected vectors and is defined as follows:
of the triangle is a linear combination of the three randomly selected vectors and is defined as follows:
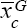 of the triangle is a linear combination of the three randomly selected vectors and is defined as follows:
of the triangle is a linear combination of the three randomly selected vectors and is defined as follows: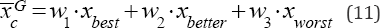
Where, the real weights wi satisfy wi≥0 and 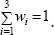 . Where the real weights wi are given by
. Where the real weights wi are given by 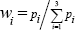 ,i= 1,2,3. Where p1=1 , and p2=rand(0.75,1) , p2=rand(0.5,p(2))
rand (a, b) is a function that returns a real number between a and b,
where a and b are not included. For unconstrained optimization problems
at any generation g>1, for each target vector, three vectors are
randomly selected, then sorted in an ascending manner according to their
objective function values and assign w1 , w2 , w3 to XGbest ,and XGbetter , XGworst respectively. Without loss of generality, we only consider minimization problem.
,i= 1,2,3. Where p1=1 , and p2=rand(0.75,1) , p2=rand(0.5,p(2))
rand (a, b) is a function that returns a real number between a and b,
where a and b are not included. For unconstrained optimization problems
at any generation g>1, for each target vector, three vectors are
randomly selected, then sorted in an ascending manner according to their
objective function values and assign w1 , w2 , w3 to XGbest ,and XGbetter , XGworst respectively. Without loss of generality, we only consider minimization problem.
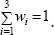 . Where the real weights wi are given by
. Where the real weights wi are given by 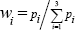 ,i= 1,2,3. Where p1=1 , and p2=rand(0.75,1) , p2=rand(0.5,p(2))
rand (a, b) is a function that returns a real number between a and b,
where a and b are not included. For unconstrained optimization problems
at any generation g>1, for each target vector, three vectors are
randomly selected, then sorted in an ascending manner according to their
objective function values and assign w1 , w2 , w3 to XGbest ,and XGbetter , XGworst respectively. Without loss of generality, we only consider minimization problem.
,i= 1,2,3. Where p1=1 , and p2=rand(0.75,1) , p2=rand(0.5,p(2))
rand (a, b) is a function that returns a real number between a and b,
where a and b are not included. For unconstrained optimization problems
at any generation g>1, for each target vector, three vectors are
randomly selected, then sorted in an ascending manner according to their
objective function values and assign w1 , w2 , w3 to XGbest ,and XGbetter , XGworst respectively. Without loss of generality, we only consider minimization problem.
In this algorithm, called IDE, the mutation rule is
combined with the basic mutation strategy through a non-linear
decreasing probability rule. A restart mechanism is also proposed to
avoid premature convergence. IDE is tested on a well-known set of
unconstrained problems and shows its superiority to state-of-the-art
differential evolution variants. Furthermore, the triangular mutation
has been used to solve unconstrained problems [38], constrained problems [39-41] as well as large scale problems [42]. Recently, In order to utilize the information of good and bad vectors in the DE population, Mohamed & Mohamed [43]
proposed adaptive guided Differential Evolution algorithm (AGDE) for
solving global numerical optimization problems over continuous space. In
order to utilize the information of good and bad vectors in the DE
population, the proposed algorithm introduces a new mutation rule. It
uses two random chosen vectors of the top and the bottom 100p%
individuals in the current population of size NP while the third vector
is selected randomly from the middle (NP-2(100p%))individuals. This new
mutation scheme helps maintain effectively the balance between the
global exploration and local exploitation abilities for searching
process of the DE. The proposed mutation vector is generated in the
following manner:
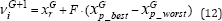
Where, xGr is a random chosen vector from the middle (NP-2 (100p%)) individuals, xGp_ best and xGp_ worst
are randomly chosen as one of the top and bottom 100p% individuals in
the current population, respectively, with p∈(0%,50%), is the mutation
factors that are independently generated according to uniform
distribution in (0.1,1). Really, the main idea of the proposed novel
mutation is based on that each vector learns from the position of the
top best and the bottom worst individuals among the entire population of
a particular generation. Besides, a novel and effective adaptation
scheme is used to update the values of the crossover rate to appropriate
values without either extra parameters or prior knowledge of the
characteristics of the optimization problem. In order to verify and
analyze the performance of AGDE, Numerical experiments on a set of 28
test problems from the CEC2013 benchmark for 10, 30, and 50 dimensions,
including a comparison with classical DE schemes and some recent
evolutionary algorithms are executed. Experimental results indicate that
in terms of robustness, stability and quality of the solution obtained,
AGDE is significantly better than, or at least comparable to
state-of-the-art approaches. Besides, in order to solve large scale
problems, Mohamed [41]
proposed enhanced adaptive differential evolution (EADE) algorithm for
solving high dimensional optimization problems over continuous space. He
used the proposed mutation [44]
with a novel self-adaptive scheme for gradual change of the values of
the crossover rate that can excellently benefit from the past experience
of the individuals in the search space during evolution process which,
in turn, can considerably balance the common trade-off between the
population diversity and convergence speed. The proposed algorithm has
been evaluated on the 7 and 20 standard highdimensional benchmark
numerical optimization problems for both the IEEE CEC-2008 and the IEEE
CEC-2010 Special Session and Competition on Large-Scale Global
Optimization. The comparison results between EADE and its version and
the other state-of-art algorithms that were all tested on these test
suites indicate that the proposed algorithm and its version are highly
competitive algorithms for solving large-scale global optimization
problems.
Practically, it can be observed that the main
modifications, improvements and developments on DE focus on adjusting
control parameters in an adaptive or self-adaptive manner.However, a few
enhancements have been implemented to modify the structure and/or
mechanism of basic DE algorithm or to propose new mutation rules so as
to enhance the local and global search ability of DE and to overcome the
problems of stagnation or premature convergence.
Conclusion
Over the last decade, many EAs have been proposed to
solve optimization problems. However, all these algorithms including DE
have the same shortcomings in solving optimization problems. These short
coming are as follows:
i. Premature convergence and stagnation due to the
imbalance between the two main contradictory aspects exploration and
exploitation capabilities during the evolution process,
ii. Sensitivity to the choice of the control
parameters which are difficult to adjust for different problems with
different features,
iii. Their performances decrease as search space
dimensionality increases. Consequently, to overcome these obstacles, a
considerable number of research studies have been proposed and developed
to enhance the performance of DE, and they can be classified into three
categories.
o Using adaptive or self-adaptive mechanisms to adapt
strategies and parameters of DE combined with single search operator or
multiple search operators
o Controlling the population diversity of DE by
introducing new parameters to measure the diversity during the evolution
process.
o Hybridizing DE with another evolutionary algorithm or classical method or incorporating local search techniques.
Although all of the above method can probably enhance
the performance of Basic DE, they definitely increase the complexity of
the algorithm by introducing extra parameters and/or complicated
mechanisms. Nonetheless, so far, there have been a few attempts in the
literature to introduce novel mutations that can balance the general
trade-off between the global exploration and local exploitation with
fast convergence speed.
For more open access journals please visit: Juniper publishers
For more articles please click on: Robotics & Automation Engineering Journal


Comments
Post a Comment