Properties of Inertial Torques Acting on Gyroscopes- Juniper Publishers
Juniper Publishers- Journal of Robotics
Abstract
The gyroscopic devices are primary arrangements for
navigation and control systems that the contemporary aerospace, ships
and other industries have been widely adopted. The main remarkable
property of the gyroscope is represented in permanent maintaining the
axis of a spinning rotor in a space. This gyroscope property is the
result of action of the several internal inertial torques produced by
the external load torque. Internal inertial torques of the gyroscope are
generated by action of the components of centrifugal, common inertial
and Coriolis forces as well as the change in the angular momentum. These
inertial forces are produced by rotating mass elements and the center
mass of the spinning rotor. The action of all gyroscope’s internal
torques are interrelated simultaneously around gyroscope axes, and are
manifested the resistance and precession torques. The designers of
gyroscopic devices can compute their acting forces and motions based on
equations of the internal torques. However, gyroscope’s inertial torques
possess several properties, which correct usage enables getting correct
results in computing of gyroscope parameters. This manuscript describes
the properties of the inertial torques acting on a gyroscope that
should be used for mathematical models of the gyroscope motions.
Keywords: Gyroscope theory; Torques; Motions; ForcesNomenclature

Introduction
From ancient time, the gyroscope was perplexing
object because it moves in peculiar and intricate ways. Scientists
become interested of its dynamics and famous mathematician L. Euler
first laid the fundamental principle for the gyroscope theory in 1765.
At those distant past the gyroscope effects were object of interest for
brilliant scientists I. Newton, J-L. Lagrange, L. Poinsot, J.L.R.
D'Alembert, P-S. Laplace, L. Foucaultand others that added new
interpretations for gyroscope properties. The interesting and remarkable
property of a gyroscope is its ability permanently maintain a reference
direction in space that later was used in engineering. The profound
interest to the gyroscope have emerged after industrial revolution, when
gyroscope properties were investigated by researchers and published in
scientific transactions [1-5].
The special gyroscope properties of a gyroscope make them extremely
important in aerospace and ships industriesespecially for advanced
navigation and control systems.
From the past century, innumerable publications and
dozen theories were dedicated to applications of the gyroscope effects
in engineering for mechanisms, devices and arrangements with the
rotating parts [6,7].
Thegyroscope theory is the compulsory chapter in the fundamental
textbooks of classical mechanics, particularly machine dynamics [8-10].
Nevertheless, the research transactions and textbooks do not fully
explain the dynamics and physics of the gyroscope properties and its
strange acting forces and motions still remain not adequately clear [11-12].
Contemporary high-tech engineering with the
gyroscopic devices use for solutions of acting forces and motions the
severe numerical models based on Lagrangian dynamics that is solved with
computer's software [13].
This is forced solution. However, allknown mathematical models for
gyroscope forces and motions contain assumptions and simplifications
that cannot give correct results. The gyroscope effects and properties
are described only by terms of the conservation of internal kinetic
energy and by the action of the change in the angular momentum that is
not enough for full explanation of properties [14-16].
Researchers intuitively pointed that the gyroscope effects and
properties are the results of the action of the inertial forces, which
are not represented by mathematical models. This is the reason that
known mathematical models for the gyroscope properties do not match
practical results [17,18].
Such situation with a gyroscope generated artificial terms as gyroscope
resistance, gyroscope couple, gyroscope effects andothers, andeven seem
to defy gravity and known physical laws. Unsolved gyroscope problems
represent challenges for scientists that every year publish around
hundred research results and discover new properties for gyroscopic
devices [19,20].
New investigations of the physical principles of
gyroscope effects show that their nature is presented by the inertial
forces of the mass elements of the spinning rotor. The gyroscope effects
and properties are the results of acting centrifugal, common inertial
and Coriolis forces as well as changes in the angular momentum of
spinning rotor. All inertial forces generate the gyroscope's resistance
and precession torques that are interrelated and occur at one time. The
physics and mathematical models of these inertial torques are well
described [21-23].
The gyroscopic devices can have different designs and
can work at different conditions with several external loads. Computing
the forces and motions for such conditions of gyroscope work is complex
problem. This paper represents the analytical approach for the
gyroscope motions around axes and describes properties of the inertial
torques acting on a gyroscope. Themathematical model describes the
action of the forces and motions accurately and validates by practical
tests and furthermore gives explanation to the gyroscope properties.The
mathematical model for the gyroscope motions under action of one load
was tested on the Super Precision Gyroscope (Brightfusion Ltd,
Abbeymead, UK).
Methodology
Recent analytical research into the physical
principles of gyroscope effects have expressedthe new mathematical
models forinertia forces acting in a gyroscope. These research results
show that the origin of actual gyroscopic effects is more complex than
presented in current publications. The action of the external load on a
gyroscope around one axis that generates several internal resistance and
precession torques acting around different axis. Equations of internal
torques are shown in Table 1.
Resistance torque is generated by the action of the centrifugal and
Coriolis forces of the gyroscope's mass elements. The precession torque
is generated by the action of the common inertial forces (for simplicity
inertial forces) of the gyroscope's mass elements and by the well-known
torque that is generated by the change in the angular momentum of the
spinning rotor. These resistance and precession torques act
simultaneously and interdependently, and are strictly perpendicular to
each other around their axes [23].

Table 1 contains the following symbols: J is the rotor's massmoment of inertia around the spinning axle; ωi is the angular velocity of precession of a spinning rotor around axis i
and ® is the angular velocity of a spinning rotor. The following
analysis of the actions of several torques and motions around the two
axes is used the system of subscripts signs. All components of the
equations are marked by subscript signs that indicating the axis of
action. For example, Tcr,x is the Coriolis torque acting around axis ox , ωy is the angular velocity of precession around axis oy , etc.
The external load torque acting on the gyroscope
around one axis is generated the several internal torques acting around
two axes. New mathematical models of the internal torques have
discovered new gyroscopic properties and behavior of gyroscopic devices.
All these inertial torques represent one system that is originated by
the action of rotating mass-elements of the spinning rotor. Motions of
the mass- elements in space generate inertial forces simultaneously
acting in different directions at the same time. Action of any internal
inertial force cannot be separated from the system of forces. Hence,
several internal torques are manifested on the resistance and precession
torques acting around two axes of a gyroscope. This is physical and
fundamental principles of the gyroscope theory. The new equations for
gyroscope internal torques enable formulating any mathematical models
for the motions of the gyroscopic devices. This analytical approach
allows the gyroscope properties and their physics to be described
clearly by known laws of classical mechanics.
The formulated new equations for the resistance and
precession torques that generated by one external torque being applied
to the spinning rotor, show that these torques at defined proportion
depend on the mass moment of inertia of a rotor and angular velocity of
the spinning rotor, as well as on the angular velocity of its
precession.
The torques generated by the centrifugal and inertial
forces is represented by one equation. However, the action of these
torques applied to different axis of the spinning rotor which
perpendicular each other. The analytical expression of this equation
describes two different properties of two torques. This is unusual
mathematical model and at first sight contradicts to rules of classical
mechanics, but analytical development and physics of action of these
torques is correct.
The external torque applied on a gyroscope produces
the resistance torques generated by the centrifugal and Corioils forces.
The torques generated by the inertial forces and by the rate change in
the angular momentum are represented the precession torque. All torques
represent one indivisible system that acting simultaneously and
interdependently on a gyroscope. Separation of action of some torque
from this system is impossible.
Equations in Table 1 represent the internal torques of the spinning rotor that are generated by the external or load torque T
. The action of the external and internal torques in the gyroscope is
represented the sequence chain of torques that activated according to
the turn around axes. The load torque generates the internal torques and
leads to manifestation of the gyroscope several properties that should
be considered in sequence of action around axis. Figure l
represents the spinning rotor that locates symmetrically relatively its
supports and shows the load and internal torques acting in the
gyroscope.
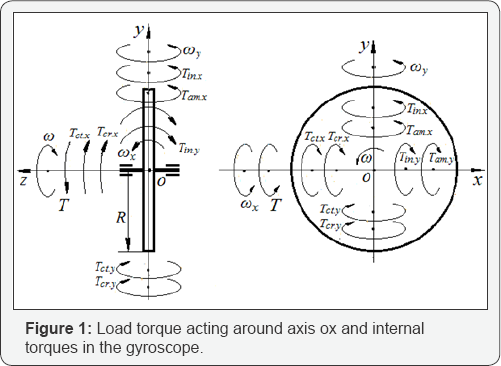
The following steps of their manifestation consider the sequence action of the torques and gyroscope motions around axes:
The gyroscope turns around axis ox
• The load torque T activates the resistance torques (Tct,x and Tcr,x
) that generated by the centrifugal and Coriolis forces, which are
restraint torques that suppress the action of the load torque and acting
around axis ox .
• Resistance torques (Tct,x and Tcr,x ) act opposite the action of the load torque T , but motion of the gyroscope at direction of the load torque.
• The load torque T activates the precession torques (Tin,x and Tam,x ) that generated by the inertial forces and the change of the angular momentum, which are load torques that
that are acting around axis oy. The resistance (Tct,x and Tcr,x ) and precession (Tin,x and Tam,x ) torques are acting around axes ox and oy respectively and simultaneously, and have one angular velocity of precession ωx. The action of these torques generated by one external torque T that cannot be separated.
The gyroscope turns around axis oy
• The precession torques (Tin,x and Tam,x ) that acting around axis oy generates the resistance torques (Tct,y and Tcr,y ) of centrifugal and Coriolis forces acting around axis oy .
• The precession (Tin,x and Tam,x ) and resistance (Tct,y and Tcr,y ) torques acting around axis oy are generated the precession torques ( Tin,yand Tam,y ) of inertial forces and the change in the angular momentum
• Acting around axis ox . This precession torques (Tin,y and Tam,y) act opposite direction to the load torque T . The resistance torques (Tct,y and Tcr,y ) and the precession torques (Tin,y andTam,y ) in sum act opposite direction to the load torque T .
The action of the internal inertial torques in the
gyroscope is the demonstration of interdependency and simultaneous
action of its external and internal torques. Any change in values of
internal torques originated at one axis lead to change in values of
internal torques of other axis and vice versa. This statement expresses
the equality of the kinetic energy of the spinning rotor which
originated and distributed equally along the gyroscope axes ox and oy
. Internal torques, angular velocities of precessions and angular
velocity of spinning rotor express the internal kinetic energy of the
rotor that is constant for the given data of the gyroscope.

The action of the external torque on a gyroscope
generates two resistances and two precession torques acting
simultaneously and interdependently around two axes that strictly
perpendicular to each other. This dual action of the external torque and
interrelation of internal torques cannot be expressed and linked by
mathematical equations.Represented properties and conditions of the
gyroscope functioning demonstrate that all components of equations (Table 2)
are interrelated each other and constant for the given gyroscope
parameters. This property ofthe gyroscope does not contradict to
principles of classical mechanics.
Represented above gyroscope's properties have defined
explanations of their physics. Mathematical models of gyroscope torques
and motions based on new analytical approaches are validated by
practical tests. The internal torques that originated along each axis
express the internal kinetic energy. The sum of these internal torques
of one axis in absolute value is equal to the sum of the internal
torques in absolute value of another axis. The actions of the internal
torques originated along axes are not coincided with actions around
axes. The resistance and precession torques are acting around two
different axes. The equality of the internal kinetic energies of the
spinning rotor two axes is represented by the equation of the action of
the torques acting around axes ox and oy. This analytical expressionis
represented by the following equation (Figure 1):
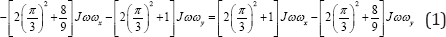
where the sign (-) and (+) means the clockwise and
counter clockwise directions of action the internal torques around two
axes, respectively.
Simplification of Eq. (1) yields the following result:
ωy = -(4π2 + 17)ωx (2)
Equation (2) demonstrates the actual ratio of the
angular velocities of the gyroscope around two axes. Analysis of Eq. (2)
shows the following peculiarity.Each axis contains resistance and
precession torques only that originated on different axes, but these
torques acting around two different axes and cannot be separated.
Resistance torques of one axis are combined with precession torques of
other axis, which actions can be contradicted. These combinations of
internal inertial torques can change the magnitudes of the angular
velocities around axes, but internal kinetic energies of each axis in
absolute values remain constant in time according to the principle of
conservation of mechanical energy. This statement enables the
combination of the internal kinetic energies of the gyroscope around two
axes to be described. The change in the value of external torque leads
to change in value of internal kinetic energy of two axes. The values of
internal torques are always less than the value of the permanent
external torque that generates the internal kinetic energies around
axes. Analysis and practical observation of the acting gyroscope with
external load torque demonstrates the following properties:
a. For the permanent external torque, the internal
kinetic energy of the spinning rotor is constant and depends on the
angular velocity of the spinning rotor ω and angular velocity of
precession m around axis ox (Figure 1). The product of these two angular velocities always constant, ωωx = const
. Increasing or decreasing the angular velocity of the rotor leads to
decreasing or increasing the angular velocity of precession
respectively.
b. The value of the internal torques and hence the angular velocity of precession ωx depends on the value of the external torque, on the rotor's mass moment of inertia and angular velocity of precession.
c. For the given value of the external torque and
angular velocity of the rotor, there is limit of the angular velocity of
precession ωx.
d. Increasing the value of the external torque, while
the angular velocity of the rotor is constant, leads to lose the ratio
of the angular velocities of precession around two axes (Eq. 2).
e. The resulting internal torque acting around axis ox generates the resulting internal torque acting around axis oy that is manifested in the form of precession motions around axesthat values are significantly different.
f. Blocking of the gyroscope turn around any axis leads to elimination the angular velocities of precessions (ωx= 0 or ωy = 0), i.e., all resistance and precession torques are deactivated.
g. Deactivation of the external torque (T = 0) leads
to deactivation of all resistance and the precession torques in spite of
their acting on different axes.
h. The separation of the action of some internal inertial torque on the gyroscope is impossible.
i. The action ofthe load torque T around axis oy generates the same sequence of action of the internal inertial torques as represented in Figure 1, but with different directions around axes oy and ox.
Analysis of acting internal inertial torques on the
gyroscope enables explaining the physics of these effects. At initial
condition, the precession torque is generated by the several inertial
forces and the change in the angular momentum of the spinning rotor
acting around axis oy at condition when the gyroscope turns with the
angular velocity of precession ωx around axis ox. Practically,
the gyroscope precession motion around axes ox or oy can be blocked or
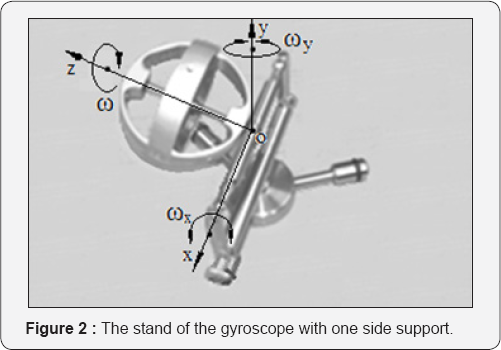
braked by action of the friction forces. Figure 2
demonstrates the stand with a runninggyroscope of one side support. The
stand assembled on the base of the Supper Precision Gyroscope
"Brightfusion LTD” that enables applying two types load acting round two
axes. The gyroscope with one side support assembled and fixed on the
centre beam with the ability to freely rotate around axis ox on the
journals of sliding bearings and that are disposed on the vertical arms
of the frame. The framedesigned with two arms and the bar with vertical
pivoted axle that disposed on the platform. The bar has the ability
freely rotate around the fixed pivot (vertical axis ) on the platform.
This stand enables blocking and braking the motions
of gyroscope around axis that demonstrating the following gyroscope
properties.
The blocking of the turn of the gyroscope around axis leads
• To stop of rotation of the spinning rotor around axis i. e., the angular velocity and acceleration is eliminated, εy =ωωx = 0 , and hence, the angular velocity of the precession around axis ox is absentωx = 0 . Then, the ratio of angular velocities around two axes (Eq. 2) is not maintained.
• The resistance torques originated and acted around axis ox are deactivated. The precession torques originated around axis ox, but are acted around axis oy .
• Since the ratio of angular velocities around two axes (Eq. 2) is not maintained, a gyroscope turns free around axis ox under action of the gravity force and generates the new internal inertial torques acting around axes ox and oy at new condition.
• As far as the gyroscope turn around axis oy is blocked, the resistance torques generated at condition of the free turn are deactivated around axis ox , but the precession torques are acted around axis oy
. This is unusual physical property of a gyroscope and manifestation of
the interdependency of all internal torques acting around two axes.
Braking the gyroscope rotation by action of the friction forces around axis oy leads
• To proportional decreasing of the value of the precession torques, which is the load torques acting around axis oy.
• An action of the resistance torques around axis oy
is result of the action the load precession torques. Hence, the value
of this resistance torques that are involved in processes also have the
same proportional decreasing.
• Decreasing of the value of the inertialtorques
acting around axis leads to same decreasing of the value for the
inertial torques around axis ox . This is result of
the interdependency of the internal torques acting around two axes that
reflects the principle of safety of the internal kinetic energy of the
spinning rotor.
• Decreasing of the value of the inertial internal
torques acting around axes and leads to increasing the action of the
torque of the gyroscope weight. Hence, the angular velocities of
gyroscope around axes ox and oy are increased.
The new analytical approach for the gyroscope
internal inertial torques describes and represents in the new light the
gyroscope properties. These properties of the gyroscope are manifested
and validated by practical tests and observation. These particularities
should be taken into account for engineering calculations of the
gyroscope problems. New analytical approach to gyroscopic problems
demonstrates that centrifugal, common inertial and Coriolis forces of
the spinning rotor are active physical components as well as the change
in the angular momentum. The latter one is one component among others
and does not play the first role in the gyroscope physics. These four
dynamical components act simultaneously and interdependently and
actually represent fundamental principles and enable formulating the
gyroscope theory. New mathematical models enable the describing all
gyroscope properties and will be useful for modelling the behavior of
the gyroscopic devices. The new analytical approach represents not only
new method of analysis with respect to a gyroscope, but also new
challenges for future studies of the gyroscopic devices.
Results and Discussion
The mathematical models for the gyroscope motions
based on action of the resistance and precession torques that are
generated by centrifugal, common inertial and Coriolis forces, as well
as by the change in the angular momentum enable the description of all
gyroscopic properties. New analytical approach to the gyroscope with
symmetrical supports and one side support enables developing the
equations for the gyroscope motions with two external load torques
acting around two axes. One load represents the action of the gyroscope
weight about horizontal axis and the other ones represents the action of
the load torque around the vertical axis. The action of these torquesis
combined with actions of the internal torques. All torques act
simultaneously and interdependently in the gyroscope. The new analytical
approach to gyroscopic problems demonstrates and explain the physical
principles of acting torques on a gyroscope and its motions. The counter
clockwise direction of the main load torque around vertical axis leads
to the clockwise turn up of the gyroscope with one side support around
horizontal axisox. This validation, that a gyroscope does not possess
the anti-gravity effect. The clockwise direction of the load torque
leads to the gyroscope turn is opposite direction. The extra load torque
of short time action leads to increasing the internal kinetic energy of
inertial torques that manifest the oscillation (galloping) of the
gyroscope. All mathematical models of the gyroscope motions with
external loads are validated the gyroscope properties by practical
observation.
Conclusion
The gyroscope theory in classical mechanics is one of
the most complex and intricate theories in terms of analytical
solutions. The known mathematical models of the gyroscope theory are
mainly based on the actions of the external load torque and the change
in the angular momentum of the spinning rotor. Numerical mathematical
models for the gyroscope motions are complex and solving by computer's
software that cannot explain the physics of acting forces. The known
approaches leadtoo many assumptions and simplifications in the case of
the unexplainable motions of the gyroscope devices. The nature of the
gyroscope motions is more complex than presented in the known gyroscope
theories. Practically, the centrifugal, common inertial and Coriolis
forces and the change in the angular momentum of the spinning rotor are
active physical components that describe all gyroscope properties. All
these forces act in the gyroscope simultaneously and interdependently
and represented the resistance and precession torques. The presentation
of the action of theseinternal torques by analytical models of the
gyroscope motions enables clear understandingthe physical process that
results in the gyroscopic devices. The new analytical to the gyroscope
problems is simple and can be used for engineering solutions of the
gyroscopic devices.The new mathematical models of internal torques
acting on a gyroscope represent fundamental principles for gyroscope
theory that can solve all gyroscope problems and represent new
challenges for future studies of gyroscopic devices.
For more open access journals please visit: Juniper publishers
For more articles please click on: Robotics & Automation Engineering Journal


Comments
Post a Comment