Recursive Parallel Nonlinear Systems Identification - Juniper Publishers

Juniper Publishers- Journal of Robotics

Abstract

Parallel nonlinear systems identification is studied. The system nonlinearity block can be noninvertible. The identification method can be dealt using hierarchical recursive least square algorithm.

Keywords: Nonlinear systems; Parallel nonlinear systems; Hierarchical method; Recursive/Iteration algorithm; Least square method

Introduction

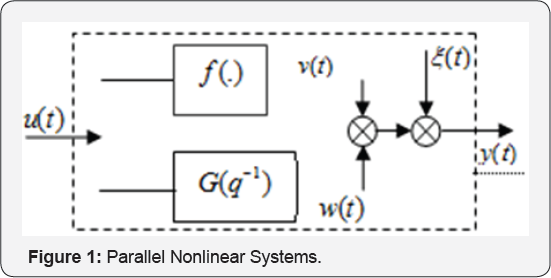
The class of nonlinear systems studied in this paper is assumed to be modelled by parallel linear-nonlinear blocks. Such model is described by parallel connection of a memory less nonlinearity and a linear dynamic blocks (Figure 1). Black-box nonlinear system identification is a very wide research area [1]. The system identification is an essential step before the control of system [2]. The considerable diversity of nonlinear systems has led to a large variety of identification problems and a proliferation of identification approaches and methods [3-5]. In the area of parameter estimation, the hierarchical identification principle based on the decomposition technique can deal with parameter estimation for multivariable systems [6].

In this paper, the problem of identifying parallel linearnonlinear block is addressed. Unlike many previous works, the nonlinearity element is of arbitrary-shape and can be noninvertible. The linear subsystem is of unknown parameters and order. Furthermore, the system nonlinearity is modeled by a linear basis function model. Some works are devoted to cancel the nonlinearity effects [7].

In most previous works devoted to parallel linear-nonlinear block system identification, the nonlinear element is supposed to be continuous. Presently, the identification algorithm is allowed to interest a wide range of the system nonlinearity. The identification problem amounts to determining an accurate estimate of the (nonparametric) nonlinearity , and the linear subsystem parameters . In this work, an identification recursive approach is dealt using hierarchical least square method to provide the system parameters estimate.

The paper is organized as follows: the nonlinear system to be identified is described in Section 2; The identification problem is formulated in Section 3; the system nonlinearity and the linear subsystem identification is coped with in Section 4; This paper will be concluded by a conclusion in Section5.

Nonlinear System Description

Standard parallel nonlinear systems consist of a memory less nonlinear element f(.) followed in series by a linear dynamic subsystem G(q_-1) (Figure 1). This model is analytically described by the following equations:

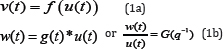
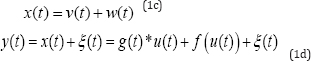
where g(t) is the impulse response of G(q_-1) ; the symbol * refers to the convolution operation; v(t) and w(t) are the output signals of the nonlinearity block and the linear subsystem block respectively is the internal signal; x(t) is the undisturbed output.

The only measurable signals are the system input u(t) and system output y(t) . The equation error ξ(t)is a zero- mean stationary sequence of independent random variables; it accounts for external noise, it is supposed to be ergodic.

Because the system identification is carried out in open loop (Figure 1), the linear block G(q_-1) must satisfy the stability asymptotically. Except for this assumption, the linear subsystem is arbitrary.

The system nonlinearity f (.) is supposed to be a nonlinear function of a known basis:

The Problem Formulation

Consider the polynomial functions A(q_-1 ) and B(q_-1) defined as follow:

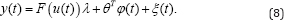
We aim at designing an identification scheme that is able to provide a model estimate of system nonlinearity as well as an estimate Ĝ(q ^-1) of linear block.

From (8) and combining the hierarchical identification principle with the least squares method, we can obtain the estimate of the nonlinear system parameters. The identification algorithm is described in the following section.

Algorithm Identification

The objective in this section is to present the steps of the nonlinear system identification. Then, from (8) and using the hierarchical identification method, the nonlinear system parameters estimate can be given using the least square algorithm. The computation process of this algorithm is summarized as:

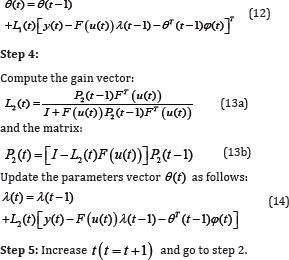
Conclusion

The problem of system identification is addressed for parallel nonlinear systems. The system nonlinearity can be noninvertible. The identification of linear block and the nonlinearity element can be achieved simultaneously using a single stage (algorithm). Presently, the proposed identification scheme can be dealt using hierarchical recursive least square approach.

To the author's knowledge, unlike many of previous study, the present method has solved the identification problem for a large class of nonlinear systems structured by blocks. Furthermore, the proposed approach involves easily generated excitation signals and few input/output data acquisition.

For More Open Access Journals Please Click on: Juniper Publishers

Fore More Articles Please Visit: Robotics & Automation Engineering Journal