Angular Parameterization of Orthonormal Wavelet Filter Banks in Power Quality: A Method for Detecting Disturbances in the Voltage Waveforms- Juniper Publishers
Juniper Publishers- Journal of Robotics
Abstract
Detecting transients in the voltage waveforms is one
of the most important issues in power quality for both the preservation
of equipment connected to the network, as well as the power supply.
Among various techniques for detection of transients in electrical
signals highlights, the wavelet transform is a method that can determine
the instant when the disturbances occur and can detect different types
in a same signal. The orthonormal wavelet filter banks yield a perfect
reconstruction of a decomposed signal and if the regularity of the used
wavelets is high, where the compression of the regular parts of the
signal is good, and better evidencing of the singularities is at hand.
In this paper, an orthonormal wavelet filter banks parameterization for
detecting disturbances in the voltage waveforms is proposed. To evaluate
the proposed methodology, some tests of detecting singularities in the
voltage waveforms are presented.
Keywords: Angular parameterization; Orthonormal wavelet; Filter banks; Power quality; Waveforms; Voltage; Electrical signals.
Introduction
The power quality is a major concern of energy
suppliers, equipment manufacturers, and users in general. Problems in
power quality can be defined as any phenomenon that occurs in voltage,
current or frequency deviation, resulting in failure or improper
operation of equipment connected to the network.
Transitional situations in power systems are common
and may occur due to lightning strikes, fault current, starting currents
of large motors, or due to capacitor switching [1].
Such disturbances that arise in the system can
cause several unwanted interference as sensitive equipment malfunction,
distortions in measurement equipment, and even they can result in the
interruption of power supply. What results in losses both for the energy
concessionaires as for the consumers. Due to the increased use of
electronic devices, it becomes increasingly necessary the care to the
energy quality provided by the power utility [2].
In this paper, a sinusoidal waveform representing
the voltage with a duration of 5 seconds is used, Figure 1, which is a
signal in its ideal form, this is, without disturbance or interference.
From this signal, the signals with disorders which is used in this work
have been generated

Short term voltage fluctuations
Variations are considered as a short term duration
when the duration is between 0, 5 cycle to 1 minute, whereas, these
voltage variations are generated by energization of large loads or
intermittent failures in the connections of the system cables. The
failures that may occur in these situations are a sag, a voltage
elevation, or complete interruption of the electrical system [2]
SAG: The voltage sag, is characterized as the occurrence of a
brief drop in the effective voltage value for a certain time interval.
Depending on the location of the fault and system conditions, a
fault may cause a temporary decrease of 10 to90% in the effective
value of the system voltage [3]. If the system voltage falls 30% or
more, its condition is considered critical [4]. It is shown in Figure
2, a sag disturbance that lasts for three cycles.
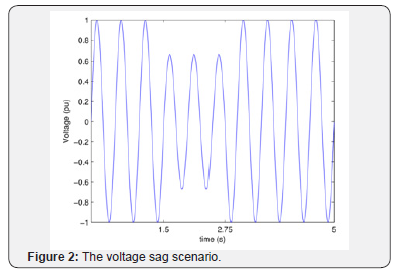
This kind of disturbances usually occur by faults in
transmission and distribution systems, and also it may arise due
to energization of heavy loads, starting of large motors or the
energizing of a transformer [2].
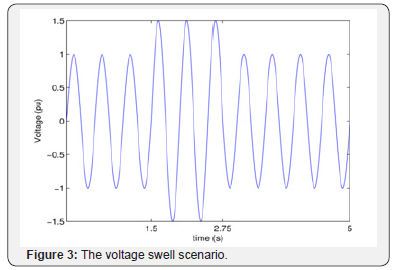
Voltage Elevation (Swell): Unlike the sag disturbance event,
the voltage elevation (Swell) is characterized by a little increase in
the system effective voltage, it is possible to occur an increase of
10% to 80% of the voltage, with duration of 0, 5cycle to 1 minute
[3]. This shortfall may stress the delicate equipment components
to premature failure.
This type of disorder can also be generated by system faults,
and mainly with the phase-to-ground short-circuit. Also it may
occur due to output of large blocks of loads or the energization
of large capacitor banks, however, with a lower incidence [2]. The
waveform of voltage swell is shown in Figure 3.
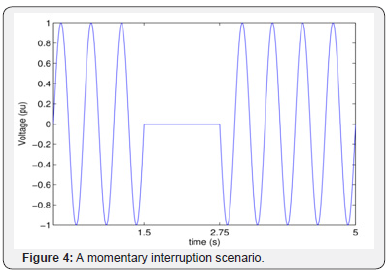
Interruption: The interruption of short duration is
characterized as a momentary loss of voltage on a power system.
An interruption which reveals a drop of 90% to 100% of the
system voltage lasting for half a cycle to 1 minute is caused by
faults in the power system, equipment failures and malfunctions
of control systems [2].
It is also possible that the interruption occurs immediately
after a voltage sag, which usually happens due to faults in the
supply system. Sag will occur between the fault inception and
operation of the protective device system. Figure 4 shows an
example of interruption applied to the presented signal of Figure
1 [2].
Long term voltage fluctuations
Voltage variations are characterized as long-term when
it occurs for a period of more than 1 minute. Having similar
characteristics with the variations of short duration and usually
caused by load variations and switching operations in the system.
Wavelet Transform - WT
The Wavelet Transform (WT) is a tool that allows the
unification of a large number of techniques for analysis and
processing. The development of wavelet theory occurred in
the fields of Mathematics, Engineering and Quantum Physics.
Currently may be included in: seismic geology, image processing,
computational and human vision, radar and sonar, spectrometry,
computer graphics, analysis of transients in power lines, and other
applications [5].
A wavelet is a function 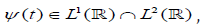 such that the
family of functions
such that the
family of functions
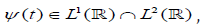 such that the
family of functions
such that the
family of functions 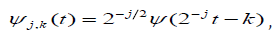
Where j and k are arbitrary integers as an orthonormal basis
for 

The Wavelet Transform is written in the form:

In (1) the values of a and b for the discrete values
a = am0 Andy are
constants has
are
constants has
 are
constants has
are
constants has
The parameter b indicates the translation of the length in
b the axis t , it is concluded that (1) provides a time-frequency
description for f . The parameter a is the scale parameter.
The function ψa,b(t) has time and width adapted to its
frequency: the ψa,b(t) under high frequency conditions is
‘narrower’, while under low frequencies, they are broad. This
makes that the wavelet transform be more efficient for local
analysis of short duration phenomena with high frequency, that
not characterize stationary signals, such as transient in signals [6].
Formulation of sherlock & monro
The angular parameterization of orthonormal filter bankwas
initially studied in [7], adapting the work of [8] infactorization of
paraunity matrix and parameterizing the orthonormal wavelet
space by a set of angular parameters. This parameterization can
be used to adjust the wavelet, in order to improve the performance
index of certain applications related to signal processing
concerned.
The weights of the low-pass filter H and high-pass filter of the
filter bank are  , and the transfer functions of these
filters are given respectively by
, and the transfer functions of these
filters are given respectively by
 , and the transfer functions of these
filters are given respectively by
, and the transfer functions of these
filters are given respectively by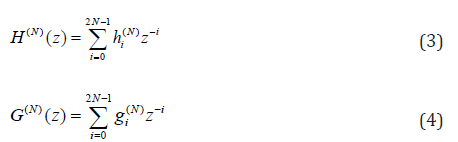
where the length of the filter bank is 2N .
To ensure the condition of complementary between H and G ,
so that the FWT is invertible, the weights of gi(N ) are obtained from
hi(N ) through a method called of ‘AlternateFlip’ in [9] as follow,
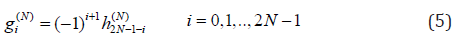
It follows that the orthogonal filter pairs can be completely
parameterized by N angles αi,1 ≤ i ≤ N , that can take anyvalue in
the set of real numbers, [10].
In the formulation of [7] and using [8], a recursive formulas to
express the coefficients of hi(N ) are presented

where i = 0,1,..,2N −1.
According to [11-13], the parameterization based on (6)
satisfies the conditions for orthonormality presented in [9],

Regularity of sherlock & monro wavelets
An important factor to be considered is the choice of the
wavelet that should be used in the analysis of a given signal. In
the decomposition of a signal by WT, properties such as regularity,
smoothness and compact support are deterministic in the choice
of wavelet to be used. The greater the number of vanishing
moments of a wavelet, the smoother it is.
The formulation of [7] guarantees the orthonormality of
the filter bank, on the other hand, it does not guarantee that the
parameterized wavelet has a number of pre-determined vanishing
moments; in this sense, [10] extend the formulation and present
restrictions to guarantee up to two vanish moments and in [11-
13] the authors has made the extension to vanishing moments of
at least three.
According to [7], in order to characterizing the WT filter bank
and considering at least one vanishing moment it is necessary to
taking into account the (9).

In order that the WT has at least two vanishing moments it is
necessary to consider (10).
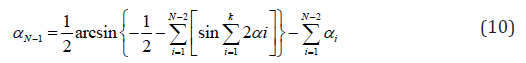
Equation (10) has a real solution if the angles i α
satisfy the
condition of (11).
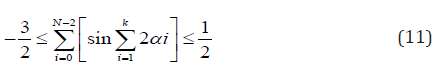
According to [11-13], continuing with the reasoning, in order
to obtain a third vanishing moment it is necessary to satisfy (12)
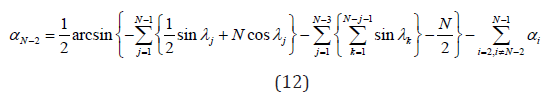
where 

The equation (12) ensures the third vanishing moment, but
the equation (12) has a real solution if the angles i α
satisfy the
condition of (13)

Detection of the Aggregated Disorders in the Voltage Waveforms
According to this idea and the previous restrictions,
especially (12), a wavelet was obtained with three null moments.
This wavelet is given from the set of angular parameters
α = {−0.3033,−0.8243,1.6308,0.2822} and is denoted by ψ , which is
shown in Figure 5.

First, the signal presented without disturbances, Figure 1, was
analyzed using ψ . The Figure 6 shows the detail coefficients of the
analyzed signal in the first (d1) and second (d2) decomposition
levels usingψ . In the Figure 7, the scalogram which represents the
percentage of energy for each wavelet coefficient is considered
[14].
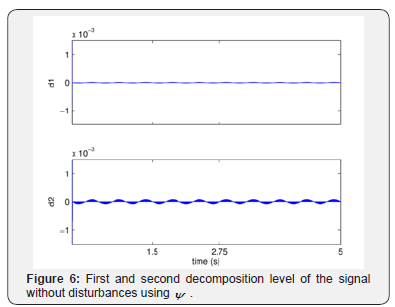

In the Figure 6, it can be seen that there is no presence of the
detail coefficients with higher amplitude suggesting the absence
of high frequency information. The concept of Figure 7 is the
same as Figure 6, because there is no evidence of energy change
at different times. This is expected since the signal is decomposed
into ideal conditions, that is, without disturbances.
After analyzing the signal without disturbances, the analysis
of signals with SAG, swell and interruption are made. In these
cases the presented singularities in the voltage waveforms should
be located according to the time in which they occur
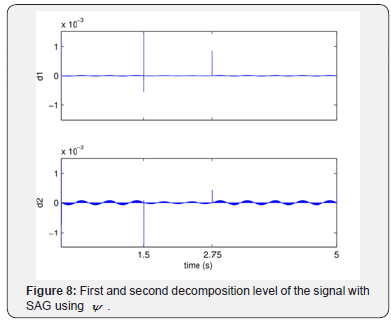
Figure 8 reveals the presence of detail coefficients with
greater amplitude at instants 1.5s and 2.75s, interval in which the
SAG phenomenon occurs. The other parts of the signal are more
regular, but in the interval 1.5s < t < 2.75s the amplitude of the
detail coefficients is slightly smaller which in 0s ≤ t < 1.5s and
2.75s < t ≤ 5s. The Figure 9 is the best evidence of it, because it
is observable that the percentage of energy in the range 1.5s < t <
2.75s is lower than of 0s ≤ t < 1.5s and 2.75s < t ≤ 5s, indicating the
presence of a dip in the signal. Therefore through both figures it
is concluded that at 1.5s minute starts a SAG which ends in 2.75s.



The signal with swell, Figure 3, was also analyzed using
the waveletψ , Figure 5, with three vanishing moments. The
decomposed signal in the first (d1) and second (d2) level is shown
in the Figure 10. In the Figure 11 the scalogram is considered which
represents the percentage of energy for each wavelet coefficient.
From Figure 10 the presence of detail coefficients with greater
amplitude at instants 1.5s and 2.75s, interval in which the swell
phenomenon occurs is realized. The other parts of the signal are
more regular, but in the range 1.5s < t < 2.75s the amplitude of the
detail coefficients is slightly lower which 0s ≤ t < 1.5s and 2.75s <
t ≤ 5s. From Figure 11 it is more understandable the meaning of
it, because it is observable the percentage of energy in the range
1.5s < t < 2.75s is higher than in 0s ≤ t < 1.5s and 2.75s < t ≤ 5s,
indicating the presence of a swell in the signal. Therefore through
both figures we conclude that the instant 1.5s minute starts a
swell which ends in 2.75s.
The signal with an interruption, Figure 4, was analyzed using
the wavelet ψ , Figure 5, with three vanishing moments. The
decomposed signal in the first (d1) and second (d2) level is shown
in the Figure 12. In the Figure 13 the scalogram is considered which
represents the percentage of energy for each wavelet coefficient.
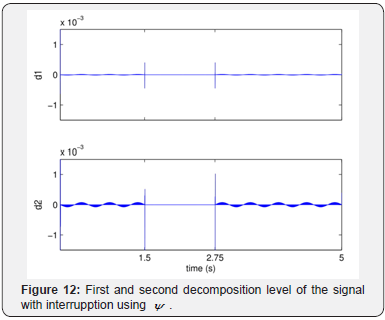
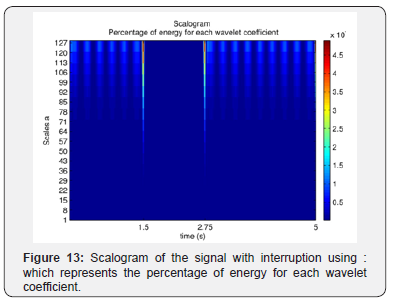
In the Figure 12 the presence of f detail
coefficients with
greater amplitude at instants 1.5s and 2.75s, interval in which
the interruption occurs is realized. The other parts of the signal are
more regular, but in the interval 1.5s < t < 2.75s the amplitude
of the detail coefficients is zero differently that in 0s ≤ t < 1.5s
and 2.75s < t ≤ 5s. The Figure 13 shows better the meaning of it,
because it is visible the percentage of energy in the interval 1.5s <
t < 2.75s is zero, as opposed that in 0s ≤ t < 1.5s and 2.75s <
t ≤ 5s,
indicating the presence of an interruption in the signal. Therefore,
from Figures 12 & 13 we conclude that at the instant 1.5s starts an
interrupt ending on 2.75s.
Conclusion
In this paper, signals with disturbances in the voltage
waveform presented in the study of power quality are analyzed.
To ensure the operation of equipment connected to the network
the detection of these disorders is important, so it is interesting
to develop efficient techniques to detect and identify the types of
disorders.
The presented method for detecting disturbances in
the voltage waveforms using angular parameterization of
orthonormal wavelet filter banks with regular functions shows a
good performance. For all the analyzed cases, the detection was
accurate, showing the beginning and end of the disorder, of cases
in which they are present in the signal.
The scalogram signal decomposed by the same wavelet with
three vanishing moments reveals the nature of the phenomenon
that occurs in the signal, since visually the detail coefficients at
different parts of the signal may look the same when it does not
identify high frequency information.
For More Open Access Journals Please Click on: Juniper Publishers
Fore More Articles Please Visit: Robotics & Automation Engineering Journal


Comments
Post a Comment