Control Parameters in Differential Evolution (DE): A Short Review- Juniper Publishers
Juniper Publishers- Journal of Robotics
Abstract
Differential Evolution (DE) is a population based
stochastic search algorithm for optimization. DE has three main control
parameters, Crossover (cr), Mutation factor (F) and Population size
(NP). These control parameters play a vital and crucial rule in
improving the performance of search process in DE. This paper introduces
a brief review for control parameters in Differential evolution (DE).
Keywords: Differential evolution; Population size; Global optimization; Control parameters
Abbrevations: DE: Differential Evolution; Cr: Crossover; NP: Population Size; F: Mutation Factor
Introduction
Differential Evolution (DE) is a population-based
heuristic algorithm proposed by Storn & Price [1] to solve global
optimization problems with different characteristics over continuous
space. Despite its simplicity, it proved a great performance in solving
non-differentiable, non-continuous and multi-modal optimization problems
[2]. DE has three main control parameters which are the crossover (CR),
mutation factor (F) and population size (NP). The values of the control
parameters affect significantly on the performance of DE. Therefore,
the tuning of those control parameters is considered a challenging task.
DE has a great performance in exploring the solution space and this is
considered as the main advantage, on the other side, an obvious weak
point is its poor performance in exploitation phase which may cause a
stagnation and/or premature convergence.
The next section introduces differential evolution.
Section 3 introduces a short review for control parameters in DE. And
finally, the paper is concluded in section 4.
Differential Evolution
In simple DE, DE/rand/1/bin [1,2], an initial
population of NP individuals jX, j=1,2,..,NP, is generated at random
according to a uniform distribution within lower and upper boundaries
(,)LUjjxx. Individuals are evolved by the means of crossover and
mutation to generate a trial vector. The trial vector competes with his
parent in order to select the fittest to the next generation. The steps
of DE are:
Initialization of a population
Initial population in DE, as the starting point for
the process of optimization, is created by assigning a random chosen
value for each decision variable in every vector, as indicated in
equation (1).
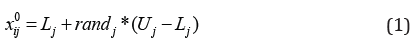
Where Lj,Uj: the lower and upper boundaries for xj, rj and: a random number uniform [0, 1].
Mutation
A mutant vector viG+1 is generated for each target vector xiG at generation G according to equation (2)
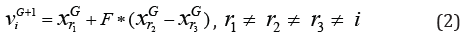
Where r1,r2, r3
are randomly chosen from the population. The mutation factor F∈[0,2]. A
new value for the component of mutant vector is generated using (1) if
it violates the boundary constraints.
Recombination (crossover)
Crossover is the process of swapping information
between the target and the mutated individuals using (3), to yield the
trial vector uiG+1 Two types of crossover can be used, binomial crossover or exponential crossover.

where j =1, 2,.., D , rand( j)∈[0,1] is the jth evaluation of a
uniform random number. Crossover rate (CR) is between 0 and 1,
r and (i) is a random index between 1 and D to ensures that uiG+1;
gets at least one element from viG+1; otherwise, the population
remains without change.
In the exponential crossover, a starting index l and a number
of components w are chosen randomly
from the ranges {l,D}and {l,D −1}respectively. The values
of variables in locations l to l + w from viG+1 and the remaining
locations from the xiG are used to produce the trial vector uiG+1
Selection
Greedy scheme for fast convergence of DE. The child uiG+1
is compared with its parent xiG to select the better for the next
generation according to the selection scheme in equation (4).
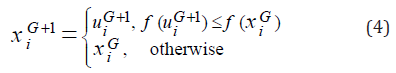
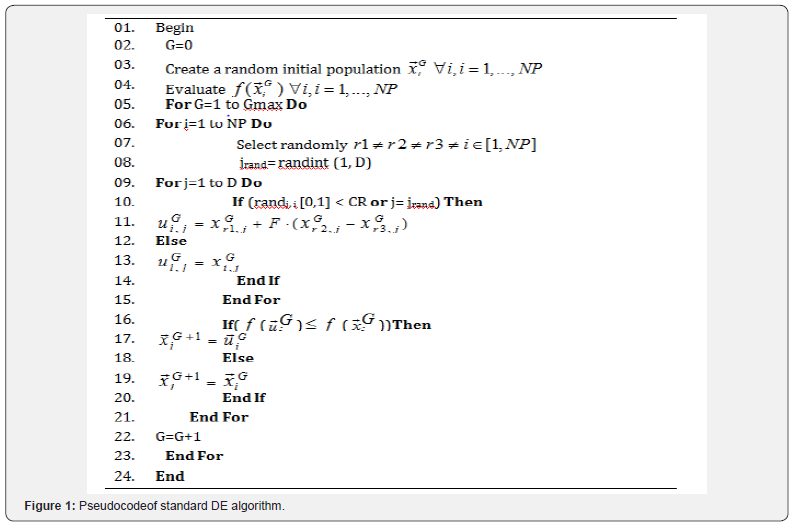
A detailed description of standard DE algorithm is given in
Figure 1.
Short Review
During the last two decades, the problem of finding the
balance between the exploration and exploitation has attracted
many researchers in order to improve the performance of DE by
developing new mutation strategies or hybridizing promising
mutation strategies.
Das et al. [3] proposed an improved variant of DE/targetto-
best/1/bin based on the concept of population members’
neighborhood. Zhang & Sanderson [4] proposed a new mutation
strategy “DE/current-to-pbest” with an optional external archive
that utilizes the historical data in order to progress towards the
promising direction and called it JADE. Qin, Huang & Suganthan
[5] proposed SaDE, in which a self-adaptive mechanism for trial
vector generation is presented, that is based on the idea of learning
from the past experience in generating promising solutions.
Mohamed et al. [6-8] proposed a novel mutation strategy which
is based on the weighted difference between the best and the
worst individual during a specific generation, the new mutation
strategy is combined with the basic mutation DE/rand/1/bin
with equal probability for selecting each of them. Li & Yin [9] used
two mutation strategies based on the best and random vectors.
Mohamed [10] proposed IDE, in which new triangular mutation
rule that selects three random vectors and adding the difference
vector between the best and worst to the better vector. The new
mutation rule is combined with the basic mutation rule through a
non-linear decreasing probability rule. And a restart mechanism
to avoid the premature convergence is presented. Recently, triangular mutation has been also used to solve IEEE CEC 2013
unconstrained problems [11], constrained non-linear integer and
mixed-integer global optimization problems [12], IEEE CEC2006
constrained optimization problems [13], CEC 2010 large-scale
optimization problems [14], and stochastic programming
problems [15].
Extensive research was presented for controlling the
parameters, as control parameters play a vital role in the evolution
process. Brest et al. [16] presented a new self-adaptive technique
for controlling the parameters. Noman & Iba [17] proposed an
adaptive crossover based on local search and the length of the
search was adjusted using hill-climbing. Peng et al. [18] proposed
rJADE, in which a weighting strategy is added to JADE, with a
“restart with knowledge transfer” method in order to benefit from
the knowledge obtained from the previous failure. Montgomery
& Chen [19] presented a complete analysis of how much the
evolution process affected by the value of CR. Mallipeddi et al. [20]
proposed a pool of values for each control parameter to select the
appropriate value during the evolution process. Wang, Cai & Zhang
[21] proposed a new method that randomly chooses from a pool
that contains three strategies in order to generate the trial vector
and three control parameter settings, they called it CoDE. Yong et
al. [22] presented CoBiDE, in which a covariance matrix learning
for the crossover operator and a bimodal distribution parameter
to control the parameters are introduced. Draa, Bouzoubia &
Boukhalfa [23] introduced a new sinusoidal formula in order to
adjust the values of crossover and the scaling factor, they called it
SinDE. A complete review could be found in [24,25].
DE mechanism depends on selecting three random individuals
from the population to perform the mutation process. Therefore,
the population size must be greater than the selected vectors.
Large population size increases the diversity but consumes
more resources (function calls), while small population size may
cause stagnation or tripping in local optima. Thus, the choosing
of the population size is considered a very critical aspect. From
the literature, it has been found that researchers choose the
population size in four different ways.
i. Choosing the population size for each problem separately
based on the experience or previous knowledge and keep it
constant during all runs [26,27].
ii. Relate the population size to the problem dimensionality
[6,28,29].
iii. Setting the population size fixed during all runs and
independent of the dimension of the problems [22,30].
iv. Allowing the population size to vary during the runs
using adaptation rule [31-33]. A complete review of population
size could be found in [34,35].
Conclusion
Control parameters plays a vital rule in the evolution process
of the DE. Over the last decades, many EAs have been proposed
to solve optimization problems. However, all these algorithms
including DE have the same shortcomings in solving optimization
problems. One of them is the choice of the control parameters
which are difficult to adjust for different problems with different
characteristics. This paper introduced a brief review for a
considerable number of research studies that have been proposed
to enhance the performance of DE.
For More Open Access Journals Please Click on: Juniper Publishers
Fore More Articles Please Visit: Robotics & Automation Engineering Journal


Comments
Post a Comment