Nonlinear Systems Estimation in Renewable Energies- Juniper Publishers
Juniper Publishers- Journal of Robotics
Abstract
In this paper, an approach estimation of nonlinear
systems in renewable energies is studied. The system can be structured
by blocks-oriented. The proposed solution is more general and can be
easy to implement.
Keywords: Nonlinear systems; Renewable energies; Oriented blocks; Harmonics analysis
Introduction
In this work, nonlinear system used in renewable
energies is dealt. These nonlinear systems can be described by
blocks-oriented. Lately, these types of models are increasingly used
practically [1-4]. Nonlinear systems estimation parameters are a
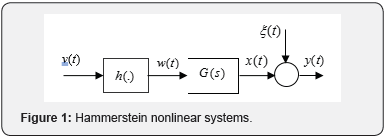
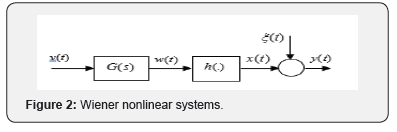
necessary step in control [5-7]. The nonlinear element can be in input
of system (Figure 1) or in output of system (Figure 2). If the two
blocks are parametric, the determination of parameters nonlinear system
can be done using quite a few solutions e.g. [1-4]. When both parts are
parametric, the identification problem has been dealt with using several
methods e.g. [1,8-10]. Two-stage nonlinear parameters estimation
solutions, involving two stages, have been established in e.g. [1,8-10].
Presently, a solution nonlinear parameters estimation is dealt. The
considered nonlinear system has a nonlinear element in output of system
(Figure 2).
These nonlinear models can describe several
industrial systems [11]. These models have been much more useful to
represent nonlinear systems. In this paper, an estimation approach is
developed to determine the nonlinear and linear elements parameters
(i.e. G(s) and f(.)). The paper is organized as follows: a brief
description of the considered nonlinear system is presented in Section
2; the nonlinear system parameters (of nonlinear and linear elements)
determination is formulated in Section 3; This paper will be concluded
by a conclusion in Section 4.
Presently, the proposed nonlinear models consist of
a linear element followed in series by a nonlinear function (.)h
(Figure 1). This nonlinear system is analytically defined by the
following equations:
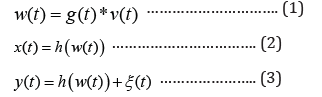
Note that the difficulty of this problem comes from
the fact that, only the input of nonlinear system v(t) and the output
signal y(t) are measurable.
The equation error ξ(t) is a stochastic sequence of
independent random variables. This signal describes the external noise.
The linear dynamic block is characterized by the amplitude ()Gjω and the
phase ()ϕω . The system n onlinearity h(.) is parametric, e.g.
polynomial function of order p. The output of nonlinear block can be
expressed as:
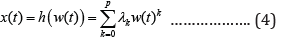
where, are the parameters of nonlinear function h(.).
In this work, the objective is to develop a solution letting the
estimation of parameters of the above nonlinear system (Figure
2) using uniquely the input signal v(t) and the output system y(t).
Nonlinear System Parameters Determination
This problem has several solutions (see please [7] and [11]).
Without loss of generalities, a very effective solution can be taken
by choosing: .
First stage
Then, applying the following signal to the nonlinear system:
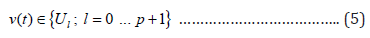
where , 0 ... 1 l U l = p + , are constant values. Accordingly, using
the chosen solution, the signal w(t) keeps the set of values:
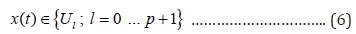
Then, the parameters estimation of nonlinear function can
be easily done using uniquely the set of input signal (5) and the
measured output signal y(t). Specifically, we have p +1 unknown
parameters corresponding to f(.), using the set of p +1 measured
points these unknowns can be covered.
First stage
At this point, the unknowns of the system that remain are the
linear element parameters ( |G( jω)| and ϕ (ω) ). For convenience,
using the input signal:

where V is arbitrarily chosen. Accordingly, using Equation (1),
the signal can be written according to the following expression:
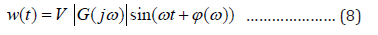
Furthermore, it is readily seen using the Equations (4) and (8)
that, the signal can expressed as:
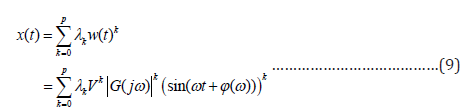
Recall that, the unknowns parameters in (9) are |G( jω)|
and ϕ (ω) (the parameters of nonlinear block h(.) λk, k =0.... p ,
are determined in the first stage).
Recall that, the unknowns parameters in (9) are G( jω)
and ϕ (ω) (the parameters of nonlinear block h(.) , 0 ... kλ k = p ,
are determined in the first stage).
Conclusion
In this work, a determination parameters approach is proposed
to estimate the parameters of nonlinear systems. The considered
nonlinear system is characterized by a nonlinear element in output
of system. In the suggested solution, two independent stages. In
the first, the nonlinear function parameters are estimated using an
easy input sequence. In the second stage, the parameters of linear
block can be covered using sine signal.
For More Open Access Journals Please Click on: Juniper Publishers
Fore More Articles Please Visit: Robotics & Automation Engineering Journal


Comments
Post a Comment